Visualizing infinity
Mathematician Hans Zantema has been emeritus professor since his retirement last September. All those who are acutely missing his lectures can now find solace in book form as Zantema has published a popular science book. All about infinite sequences, it includes the esthetically pleasing figures that surprisingly appear when these sequences are visualized. Written in Dutch, the book is entitled Spelen met oneindigheid.
Appropriately, the book comes with homework: each chapter concludes with an assignment. “Some are downright difficult, so it's no disgrace if they have you floored,” says the author – a huge puzzle fan – with a twinkle in his eye.
Hans Zantema came to work at TU/e in 2000. As an associate professor at Computer Science, he was a member of the Department of Mathematics & Computer Science. For many years he was also a full professor (part-time) at Radboud University in Nijmegen. When lecturing on computer science to students, he liked to build from a solid foundation of math.
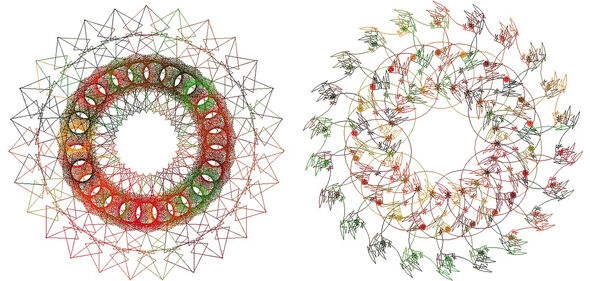
“I had a long track record of researching infinite sequences when I made a chance discovery in 2015: that you use these sequences to produce wonderful figures.” Different types of figures, in fact, including "the 'finite', which resemble a mandala, and the fractal figures, which being infinite extend in a never-ending pattern.”
Turtle
How does Zantema make the leap from a series of numbers – basically ones and zeros – to one of these images? He does this by working with the turtle figure principle. This is a step-by-step method that is used, for example, to help children learn computer programming.
“Imagine a small robot, or a turtle, that walks. After every step, it makes a turn of a certain angle depending on the next number in the infinite series. For example, when a zero comes up, it might turn 140 degrees to the left, and when a 1 comes up, it'll turn 80 degrees to the right.”
Zantema discovered that by visualizing an infinite sequence according to this procedure, he could produce beautiful pictures, “with a program consisting of just a few lines of code”. Providing he programmed the imaginary ambling robot with the correct angles.
“The math and the creation of the figures went hand in hand: establishing the correct angles gave rise to mathematical theorems that in turn led to new figures.”
Would you like to know more? In a preview (in Dutch) of his book, Zantema reveals a little of the theory.
Puzzles
Has he found his next calling? “I certainly have more time for supplementary activities now that I'm retired, although I'm still doing scientific research. I can't claim to have written another book yet, but I am translating Spelen met oneindigheid into English, so that it can potentially be published internationally.”
Some years ago, however, Zantema’s penchant for puzzles did inspire him to write another book: in 2007 he published De achterkant van sudoku, in which he explains ways to solve these popular Japanese number puzzles, and how to make them. “I also like making computer games, which I then play. They usually involve a combination of skill and math.”
Stained glass
He is intrigued to know how Spelen met oneindigheid (Playing with Infinity) will be received. “I'm quite nervous about it. It's a popular science book for a broad readership, but it's also a proper math book. And some of the puzzles in the book are really difficult.”
The early chapters focus mainly on the kind of basic math taught to math undergraduates, says Zantema. After that he takes the reader through the steps he discovered for visualizing infinity.
If the book were to catch on in the art and design world, he'd be very happy. “At my farewell party at TU/e, I was given a rather special gift by my colleagues. They had designed a figure using the method in Spelen met oneindigheid and asked an artist to recreate that image in stained glass.”
Since then, more of Zantema’s ‘infinites’ have been immortalized in stained glass. “Several students of the glass artist have created objects based on my images. I visited the glass studio while a lesson was in progress; it was quite something to see how they were using the images I had programmed as templates.”
Like to win a book?
Would you like to win Spelen met oneindigheid? Cursor has three copies (in Dutch) to give away to students and/or TU/e employees who can correctly solve the puzzle below - naturally devised by Hans Zantema himself. Send your solution to cursor@tue.nl before midnight on March 26, 2023. Zantema will judge the solutions. If more than three entries are correct, the winners will be picked out of a hat.
The puzzle is a variation of a challenge that also features in the book, and it goes as follows:
Two numbers A and B are modified indefinitely. Initially, A has value 144 and B has value 72. Then go to (1).
(1): Add B to A, then go to (2).
(2): If B is even, add 10 to A, otherwise leave everything unchanged. Then go to (3).
(3): If A is even, subtract 1 from B, otherwise leave everything unchanged. Then go to (1).
The question is: what is the largest occurring value of A during this infinitely long process? Anyone who is familiar with programming can easily write a program for this, and find the answer by running it. But the real challenge is to determine the intended greatest value of A without using other tools than pen and paper.
UPDATE 27 MARCH 2023 | The contest is closed and the correct answer, including elaboration (in Dutch) by Hans Zantema, can be found here.
Spelen met oneindigheid. Verrassende figuren en patronen | Hans Zantema | ISBN 978 94 6471 021 2 | Paperback | 240 pages | € 22,90 | Published by Noordboek







Discussion